Note: conversion to Bouwkamp notation can be done using the interactive browser.
The problem statement is simple: Given natural numbers n and m, find the minimum number of integer-sided squares that tile an (n,m) rectangle. (The problem was posed to me by David Radcliffe).
If the rectangle is a square, then obviously one square is sufficient to fill it.
If the two sides (n,m) of the rectangle have a common divisor d, then any solution for a rectangle of size (n/d,m/d) can be scaled up to a solution of size (n,m).
Another possible reduction is by splitting a rectangle of size (n,m) into two rectangles horizontally ((h,m) and (n-h,m)) or vertically ((n,v) and (n,m-v)).
Sometimes none of the reductions mentioned yields an optimal solution. The smallest such case is (13,11).
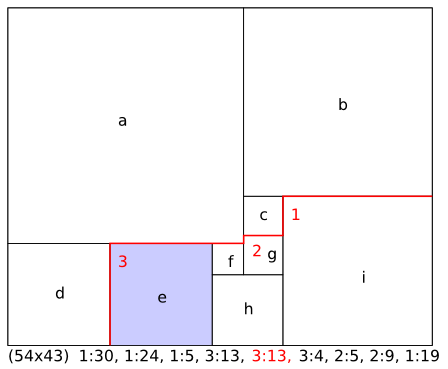
Basic solutions are represented as a sequence of pairs of numbers, each
representing a square. In each step, the area of the rectangle that
is already filled has the shape of a Young tableaux. The first number
indicates which of the top-left corners of the free area is going
to be filled. The second number is the size of the square. The
following image illustrates this for the
(54,43) rectangle.

Note: conversion to
Bouwkamp notation
can be done using the interactive browser.
Let h(n,m) be the minimum number of integer-sided squares that tile an (n,m) rectangle.
Proofs of these facts are on a separate page.
The implementations operate on sequences of so-called valleys, which may be visualized by turning a Young tableaux by 135 degrees such that the top-left corner moves to the bottom. The empty area can now be described as a sequence of lines from left to right, alternating between downwards and upwards slopes. Each pair of downward and upward slopes is a valley.
In each level of the search, one of the valleys is chosen and filled with a square. To avoid duplicate work, we also keep track of which squares have already been tried for each valley, in the form of a lower bound on the squares that may be used to fill it.
Finally, a simple heuristic is used for truncating the search tree: a sequence of n valleys needs at least n squares to be filled completely.
Rather than iterative deepening, the program searches for solutions starting from an upper bound derived from the simple reductions listed earlier. This is faster in general, but makes the runtime sensitive to the search order. It turns out (contrary to my expectations) that trying to fill valleys with small squares first finds solutions faster than starting with big squares.
| 2012-11-12 | Haskell implementation and results up to n,m ≤ 85 |
| 2012-12-02 | Reimplementation in C++, results up to n,m ≤ 144 (stopped: 2012-12-05), reconstruction of solutions, webpage |
| 2012-12-08 | Added some proofs. |
| 2013-01-04 | Ed Pegg provided results up to n,m ≤ 160! |
| 2013-02-24 | Implemented browser for solutions. (Tested on Firefox 10) |
| 2013-03-11 | Improved runtime of C++ program by factor of 20. Extended results up to 284×284, using a 48 core machine at the University of Innsbruck. |
| 2013-03-17 | Extended results up to 300×300 using the same computer. |
| 2015-09-02 | Massimo Ortolano provided results up to 321×321. |
| 2015-11-24 | Massimo Ortolano provided results up to 350×350. |
| 2016-06-14 | Massimo Ortolano provided results up to 380×380. |
| 2017-07-xx | Ed Pegg pointed out an error in row 323. Further investigation turned up wrong results in rows 323 and 352. I believe this happened due to a restart of the program that caused the search for basic solutions to be skipped for these two rows; the results in the other rows should be correct. |
| 2017-08-26 | Massimo Ortolano provided corrected results for rows 323 and 352, and further results up to 388×388. |